introduction
This page presents sample lattices for testing algorithms that solve the shortest vector problem (SVP) in euclidean lattices. The SVP challenge helps assessing the strength of SVP algorithms, and serves to compare different types of algorithms, like sieving and enumeration. The lattices presented here are random lattices in the sense of Goldstein and Mayer.
participation
How to participate:
You can either- download a sample lattice on the right side, or
- use the generator online to produce a lattice with (integer) seeds of your choice, or
- download the generator and install it with an NTL older than NTL 9.4 (necessary since NTL 9.4 and later versions use a different pseudorandom number generator) to create challenges on your local machine.
How to enter the Hall of Fame:
To enter the hall of fame, you have to submit a vector with- Higher dimension and Euclidean norm less than
(which is an estimation of the length of a shortest vector in the lattice), or
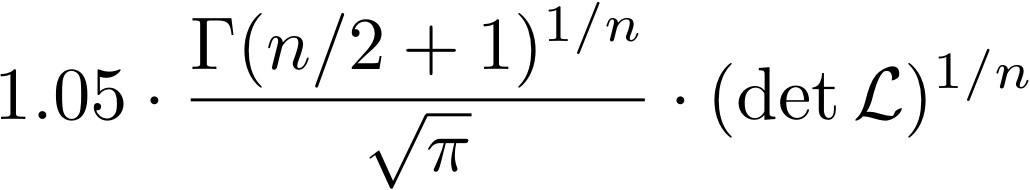
- A shorter vector than a previous one in the same dimension (with possibly different seed)
Acknowledgment:
Special thanks to Yuntao Wang and Junpei Yamaguchi for pointing out the change in the NTL pseudorandom generator and to Yuntao Wang for helping with the online version of the generator.hall of fame
| Position | Dimension | Euclidean norm | Seed | Contestant | Solution |
|---|---|---|---|---|---|
| 1 | 190 | 3613 | 0 | Yao Sun and Shuai Chang | vec |
| 2 | 186 | 3484 | 0 | Leizhang Wang, Baocang Wang | vec |
| 3 | 185 | 3580 | 0 | Wenwen Xia, Geng Wang, Dawu Gu | vec |
| 4 | 184 | 3494 | 0 | Leizhang Wang, Baocang Wang | vec |
| 5 | 183 | 3536 | 0 | Ziyu Zhao, Jintai Ding, Bo-Yin Yang | vec |