introduction
This page presents sample lattices for testing algorithms that solve the shortest vector problem (SVP) in euclidean lattices. The SVP challenge helps assessing the strength of SVP algorithms, and serves to compare different types of algorithms, like sieving and enumeration. The lattices presented here are random lattices in the sense of Goldstein and Mayer.
participation
How to participate:
You can either- download a sample lattice on the right side, or
- download the generator and generate lattices yourself
How to enter the Hall of Fame:
To enter the hall of fame, you have to submit a vector with- Higher dimension and Euclidean norm less than (which is an estimation of the length of a shortest vector in the lattice), or
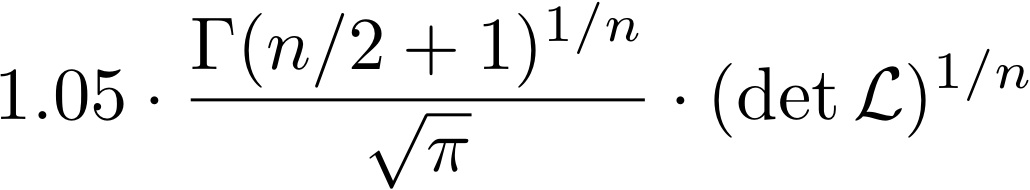
- A shorter vector than a previous one in the same dimension (with possibly different seed)
hall of fame
| Position | Dimension | Euclidean norm | Seed | Contestant | Solution |
|---|---|---|---|---|---|
| 1 | 120 | 2851 | 0 | Po-Chun Kuo, Michael Schneider | vec |
| 2 | 116 | 2825 | 0 | Po-Chun Kuo, Michael Schneider | vec |
| 3 | 114 | 2778 | 0 | Po-Chun Kuo, Michael Schneider | vec |
| 4 | 112 | 2715 | 0 | Yuanmi Chen and Phong Nguyen | vec |
| 5 | 112 | 2748 | 0 | Po-Chun Kuo | vec |